Suche
Günther Jena

Beispiel 1 - Der Paketdienst
- Am Anfang der Fahrt erhält er 20 Pakete, die er während des Tages ausliefern muss
- Fragestellung: Was ist die beste Route?
- Wieviel Möglichkeiten gibt es?
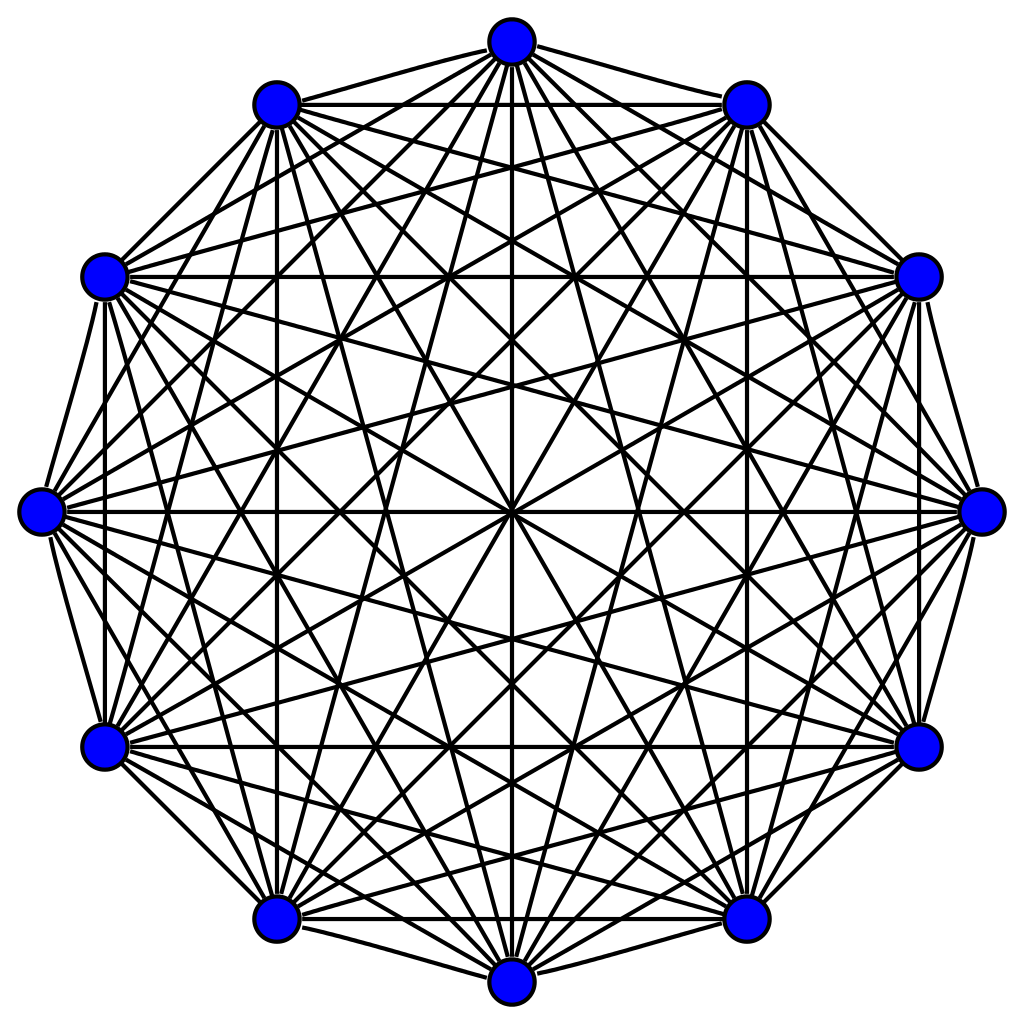
Hier die möglichen Wege für nur 11 Pakete...
Wieviel Möglichkeiten gibt es?
- Für die erste Fahrt gibt es 20 Möglichkeiten, für die zweite 19, ...
- Also gibt es 20 * 19 * 18 * 17 * 16 * ... * 2 Möglichkeiten (20!)
- 2.432.902.008.176.640.000 Möglichkeiten
Wie lange dauert die Berechnung?
- Angenommen wir schaffen 1 Milliarde Möglichkeiten pro Sekunde zu berechnen...
- ... benötigen wir über 77 Jahre
Beispiel 2 - Königsberger Brückenproblem
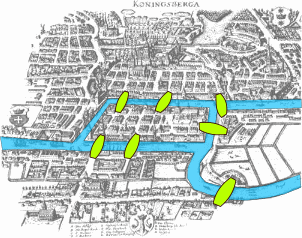
- Frage: Gibt es einen Weg, bei dem man alle sieben Brücken genau einmal überquert?
- Bonusfrage: Gibt es einen Rundweg folgend dieser Bedingung?
Leonhard Euler bewies 1736, dass ein solcher Weg nicht möglich ist.
- Es dürfte maximal zwei Ufer mit einer ungeraden Zahl von angeschlossenen Brücken geben.
- Diese zwei Ufer könnten Ausgangs- bzw. Endpunkt sein.
- Nicht möglich ist ein "Rundweg" (auch Eulerweg genannt).
Die Anfänge der Graphentheorie gehen auf dieses Problem zurück.
Graphentheorie
Ein Graph ist eine abstrakte Struktur, die eine Menge von Objekten (genannt Knoten) zusammen mit den zwischen diesen Objekten bestehenden Verbindungen (genannt Kanten) repräsentiert.
Eigenschaften von Graphen
- Kanten: gerichtet - ungerichtet, gewichtet - ungewichtet
- Zyklen
- Planar
Baum
- kreisfrei (azyklisch)
- Spezialfall: Binärer Baum - darf höchstens zwei untergeordnete Knoten haben
- Begriffe: Wurzel, Ast, Blatt
Uninformierte Suche
Breiten- und Tiefensuche
Informierte Suche
Branch-and-Bound
Unnötige Äste im Suchbaum werden nicht weiter untersucht (abgeschnitten)
A* Algorithmus
Es wird eine Heuristik (Abschätzung) verwendet, um die Suche zu optimieren
- Beispiele: Luftlinie, Kostenabschätzung, ...
- Wichtige Bedingung: Eine Heuristik muss immer optimistisch sein
A* Beispiel
Für weitere Beispiele siehe Graph Search Visualizer